TheTarPit

Modelowanie niezupełnie rzeczywiste

W najróżniejszych ogólnych opisach i wstępach do technologii mówi się często, że programowanie obiektowe przedstawia związki między pojęciami w sposób analogiczny jak to ma miejsce w świecie rzeczywistym. Dzięki temu oprogramowanie ma być bliższe prawdziwemu światu — opiera się na interakcji autonomicznych obiektów, a nie tylko na wykonywaniu jakiegoś abstrakcyjnego ciągu rozkazów. Zgodnie z tym wszelkie dodatkowe technologie, które wyewoluowały z tego paradygmatu, w szczególności UML, oferują zestaw pojęć i notacji do „modelowania świata”. Taki model przekłada się potem na klasy, które w założeniu mają reprezentować obiekty lub pojęcia rzeczywiste czy chociażby wyobrażalne oraz relacje między nimi.

Zadziwiające, jak łatwo udowodnić, że jest to bzdura... Chociażby wykorzystując stary (nawet jeśli znany, to wart przypomnienia) przykład z kwadratem i prostokątem.

Kwadrat jako prostokąt

Nie trzeba mieć szczególnie głębokiej wiedzy z zakresu geometrii ani jakoś specjalnie rozbudowanej wyobraźni żeby stwierdzić, że kwadrat to szczególny rodzaj prostokąta. Inaczej mówiąc kwadrat, to ogólnie rzecz biorąc prostokąt, tylko akurat taki, który przypadkowo oba wymiary (wysokość, szerokość) ma równe. W języku UML, który zgodnie ze wszelkimi światowymi tendencjami najlepiej wykorzystywać do modelowania rzeczywistości obiektowej, uogólnienie „kwadrat (klasa Square) to rodzaj prostokąta (klasa Rectangle)” można przedstawić następująco:

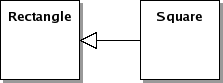
Rys.1. „Kwadrat to prostokąt” w UML

Po dodaniu do tego kilku podstawowych metod oraz przetumaczeniu na kod (tym razem Java), klasa reprezentująca prostokąt może wyglądać tak:

public class Rectangle {
  private double a;
  private double b;

  public Rectangle(double a, double b) {
    this.a = a;
    this.b = b;
  }
  public double getArea() {
    return a*b;
  }
  public double getA() {
    return a;
  }
  public void setA(double a) {
    this.a = a;
  }
  public double getB() {
    return b;
  }
  public void setB(double b) {
    this.b = b;
  }
}

Zgodnie z powyższym klasa reprezentująca kwadrat musiałaby wyglądać jakoś tak:

public class Square extends Rectangle {

  public Square(double a) {
    super(a, a);
  }
  public void setA(double a) {
    super.setA(a);
    super.setB(a);
  }
  public void setB(double b) {
    super.setA(b);
    super.setB(b);
  }
}

I teraz na diagramie UML całość wygląda następująco (ikonki i upiększenia dodane przez program Together Arhitect 2006):

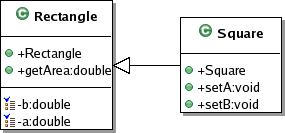
Rys.2. Uzupełniony diagram z rys.1.

Na pierwszy rzut oka widać, że coś jest tutaj nie tak. Nie możemy dopuścić do „zwichrowania” kwadratu przez zamianę długości tylko jednego boku. Zatem trzeba odpowiednio „nadpisać” setery (setA, setB). Trochę dziwnie to wygląda, ale jest jeszcze do przyjęcia...

Wyobrażmy sobie teraz, że prostokąt można skalować, oczywiście w obu kierunkach niezależnie. Wystarczy dopisać do klasy Rectangle coś w tym stylu:

  public void scaleA(double s) {
    this.a *= s;
  }
  public void scaleB(double s) {
    this.b *= s;
  }

Dziedziczenie zapewnia nam, że klasa Square teraz również ma metody scaleA i scaleB. Jednak kwadratu nie można skalować w obu kierunkach niezależnie, zatem trzeba to jakoś obsłużyć, pewnie podobnie jak zmianę rozmiaru wcześniej. Da się to oczywiście stosunkowo łatwo zrobić, ale... Następuje tu powoli eskalacja problemu. Przecież tak naprawdę kwadrat nie ma wymiaru b. Nie wystarczy, że obsłużymy to tak, aby kwadrat się nie „zwichrował” w żadnej możliwej sytuacji. Nie powinniśmy się w ogóle nad tym zastanawiać ponieważ kwadrat takiego problemu po prostu nie ma. I tyle.

Prostokąt jako kwadrat

Rozwiązanie powyższego problemu jest oczywiście banalne. Skoro konstrukcja dziedziczenia w programowaniu obiektowym oznacza, że klasa pochodna rozszerza możliwości klasy bazowej (stąd bardzo ładne słowo kluczowe extends w Javie), to należy do sprawy podejść „od dupy strony”.

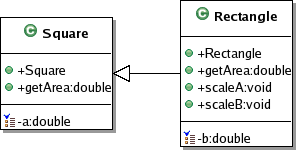
Rys.3. „Prostokąt to kwadrat” w UML

Klasą podstawową jest teraz kwadrat (Square). A prostokąt (Rectangle) „rozszerza możliwości” kwadratu dodając mu drugi, niezależny wymiar.

public class Square {
  private double a;

  public Square(double a) {
    this.a = a;
  }
  public double getA() {
    return a;
  }
  public void setA(double a) {
    this.a = a;
  }
  public double getArea() {
    return a*a;
  }
}

public class Rectangle extends Square {
  private double b;

  public Rectangle(double a, double b) {
    super(a);
    this.b = b;
  }
  public double getB() {
    return b;
  }
  public void setB(double b) {
    this.b = b;
  }
  public double getArea() {
    return super.getA() * b;
  }
  public void scaleA(double s) {
    super.setA(super.getA() * s);
    return;
  }
  public void scaleB(double s) {
    this.b *= s;
    return;
  }
}

Nowe metody w klasie Rectangle dodają nowe cechy lub funkcjonalność (jak scale...) lub modyfikują metody klasy bazowej ze względu na wymagania tych nowych cech (jak nowa postać metody getArea). Zatem z punktu widzenia programowania obiektowego jest teraz zdecydowanie lepiej.

A że rysunek 3 sugeruje jakby to prostokąt był kwadratem a nie odwrotnie...? Cóż, może z tym „modelowaniem rzeczywistości” to jednak niezupełnie jest tak prosto...

Świat niekoniecznie rzeczywisty

Rzeczywistość biologiczno-fizyczna ma swoje prawa (i miliony wyjątków, ale to inna sprawa) i podobnie próbują postępować pewne nauki ścisłe, jak np. matematyka. Jednak programowanie może mieć zupełnie inne zasady i nie zawsze jest sens odwoływać się do praw świata realnego. Bo właściwie to jest dla nas bez znaczenia, czy umówimy się, że „kwadrat to prostokąt, tylko że ma cechy szczególne (oba boki takie same)” czy też „prostokąt to kwadrat, tylko że ma cechy szczególne (boki niekoniecznie takie same)”.

Co prawda to drugie zdanie brzmi zupełnie jak „prostokąt to kwadrat, tylko że ma cechy szczególne (nie jest kwadratem)”, ale paranoja to najmniejszy ze skutków ubocznych zajmowania się tą branżą...

Komentarze

public Rectangle scaleA(double s) {
        Rectangle r = new Rectangle(this.a, this.b);
        r.setA(s * a);
        return r;
}